| Fundamentals Review | MP4 | Flash | |
| Binary Coded Decimal, Counting | MP4 | Flash | |
| Boolean Algebra | MP4 | Flash | Slide |
| Standard Forms | MP4 | Flash | Slide |
| Universal Gates | MP4 | Flash | Slide |
| Introduction to K-Maps | MP4 | Flash | Slide |
| Optimization with K-Maps | MP4 | Flash | Slide |
| Don't-Cares | MP4 | Flash | Slide |
| Decoders and Encoders | MP4 | Flash | Slide |
| Multiplexers | MP4 | Flash | Slide |
| Tristates | MP4 | Flash | Slide |
| Implementation Technology | MP4 | Flash | Slide |
| Arithmetic Structures | MP4 | Flash | Slide |
| ALUs | MP4 | Flash | Slide |
| Re-examining Carry Bits | MP4 | Flash | Slide |
| Carry Look-Ahead Adders | MP4 | Flash | Slide |
| D Latches and FFs | MP4 | Flash | Slide |
| Intro to Sequential Circuits | MP4 | Flash | Slide |
| State Diagrams | MP4 | Flash | Slide |
| Sequential Circuit Design Overview | MP4 | Flash | Slide |
| State Minimization | MP4 | Flash | Slide |
| FSM Design and Verification | MP4 | Flash | Slide |
| Flip-Flop Timing Parameters | MP4 | Flash | Slide |
| Sequential Circuit Timing | MP4 | Flash | Slide |
| One-Hot State Machines | MP4 | Flash | Slide |
| Other Flip-Flop Types | MP4 | Flash | Slide |
| Registers | MP4 | Flash | Slide |
| Register Design | MP4 | Flash | Slide |
| Intro to Complex FSMs | MP4 | Flash | Slide |
| Complex FSMs | MP4 | Flash | Slide |
| Pipelining | MP4 | Flash | Slide |
| Serial Transfers | MP4 | Flash | Slide |
| Registers with Shared Logic | MP4 | Flash | Slide |
| Basic Processor Structure | MP4 | Flash | Slide |
| Operation of a Basic Processor | MP4 | Flash | Slide |
| Intro to Memory | MP4 | Flash | Slide |
| SRAM Design | MP4 | Flash | Slide |
| SRAM Arrays | MP4 | Flash | Slide |
CS/ECE 352: Digital System Fundamentals
Source: http://ece352.engr.wisc.edu/
This tutorial walks through how you can deploy WordPress on a CS Department Server.
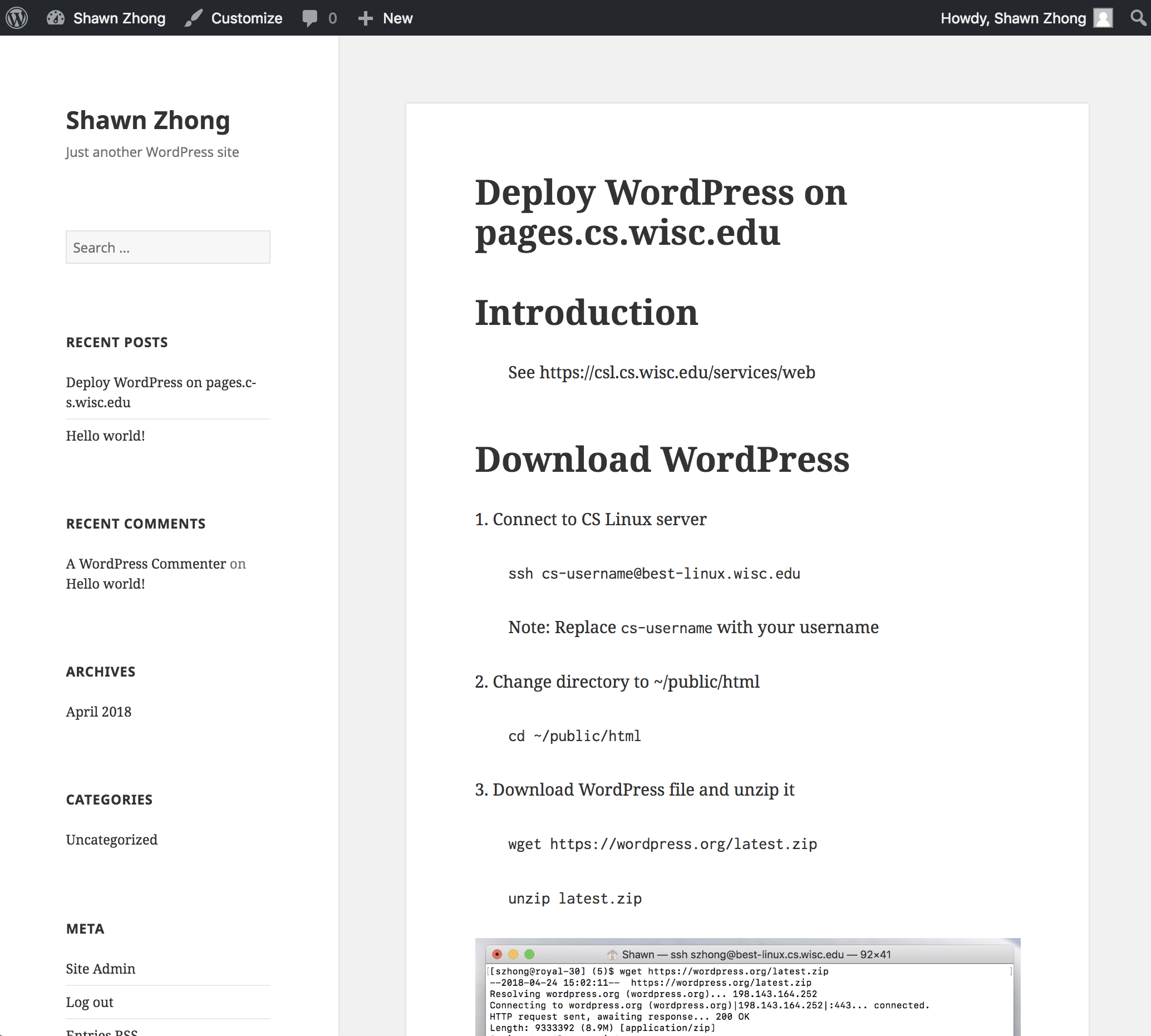 (more…)
(more…)
 (more…)
(more…)


![Ideals Generated by Subset • Definition ○ Let R be a commutative ring ○ If A is a subset of R, then the ideal generated by A is ○ (A)≔{r_1 a_1+…+r_n a_n│n∈Z(≥1),r_i∈R,a_i∈A}⊆R ○ If A is finite, then we write (A) as (a_1,…,a_n ) • Notice: when |A|=1, (A) is a principal ideal • Example: (2,x)⊆Z[x] ○ Suppose, by way of contradiction, that (2,x)=(p) for some p∈Z[x] ○ Since 2∈(p) § 2=pq for some q∈Z[x] § 0=deg2=degp+degq § degp=degq=0 ○ Since x∈(p) § Choose r∈R[x] s.t. pr=x, then deg〖r=1〗 § Write r=ax+b,where a,b∈Z § Then pr=p(ax+b)=x § So pa=1, by comparing coefficients § Since p∈Z[x] and a∈Z, p∈{±1} ○ Therefore (2,x)=Z[x] ○ So, 1=2p^′+xq′, where p^′,q^′∈Z[x] ○ Evaluating both side at 0, we get 1=2p^′ (0)=0 ○ This is a contradiction, so (2,x)⊆Z[x] • Example: Z[x]\/(2,x)≅Z\/(2) ○ Define F:Z[x]→Z\/2Z given by a_0 x^n+…+a_1 x+a_0↦(a_0 ) ̅ ○ F is a ring homomorphism § F factors as Z[x]→Z→Z\/2Z, where p↦p(0)↦p((0) ) ̅ § Composition of homomorphisms is still a homomorphism ○ F is certainly surjective ○ (2,x)⊆kerF § Let p∈(2,x) § Then p=2g+xh for some g,h∈Z[x] § Since xh has no constant term, and 2g has even constant term § F(p)=F(2g)=F(g)=0 ̅∈Z\/2Z ○ kerF⊆(2,x) § Let p∈kerF § Write p=a_n x^n+…+a_1 x+a_0 § Write a_0=2b,b∈Z § Then p=x(a_n x^(n−1)+…+a_1 )+2b∈(2,x) ○ Therefore, kerF=(2,x) ○ By the First Isomorphism Theorem of , Z[x]\/(2,x)≅Z\/2Z≅Z\/(2) ○ Note: Z[x]\/(x,n)≅Z\/(n) Maximal Ideal • An ideal M in a ring R is maximal if • M≠R, and the only ideals containing M are M and R Proposition 71: Criterion for Maximal Ideal • Statement ○ If R is a commutative ring, and M⊆R is an ideal ○ Then M is maximal ⟺R\/M is a field • Proof (⟹) ○ The only ideals containing M are R and M ○ Thus, R\/M has exactly 2 idals, by the Correspondence Theorem ○ Namely, the zero ideal, and the entire ring ○ Let x+M∈R\/M ○ Suppose x∉M i.e. x+M≠0 ○ Then (x+M)=R\/M ○ So 1+M∈(x+M) ○ Choose y+M∈R\/M s.t. (x+M)(y+M)=1+M ○ This shows x+M is a unit ○ Therefore R\/M is a field • Proof (⟸) ○ Suppose R\/M is a field ○ Then R\/M has exactly two ideals, 0 and R\/M ○ By the Correspondence Theorem, ○ There are exactly two ideals containing M: R and M ○ By definition of maximal ideal, M is maximal Examples of Maximal Ideals • What are the maximal ideals in Z? ○ (n)∈Z is maximal ⟺Z\/(n) is a field ⟺ n is prime • Is (x)⊆Z[x] maximal? ○ No, (x)⊊(2,x)≠Z[x] ○ Also, by First Isomorphism Theorem, Z[x]\/(x)≅Z, but Z is not a field § Define a ring map Z[x]→Z given by p→p(0) § F is surjective, and kerF=(x) • Is (x^2+1)⊆R[x] maximal? ○ R[x]\/(x^2+1)≅ℂ is a field • Is (x^2−1)⊆R[x] maximal ○ R[x]\/(x^2−1)≅R×R is not a field, since (1,0) is not a unit ○ Another way to see (x^2−1) is not maximal § (x^2−1)⊊(x−1)⊊R[x] § (x^2−1)⊊(x+1)⊊R[x]](https://shawnzhong.com/wp-content/uploads/2018/05/img_5aee4f89b32e7.png)
![Theorem 70: The First Isomorphism Theorem for Rings • Statement ○ If f:R→S is a ring homomorphism, then there is an induced isomorphism ○ f ̅:R\/kerf→im(f), given by r+kerf↦f(r) • Proof ○ We need only check f ̅(1_(R/kerf ) )=1_S, and f ̅ preserves multiplication ○ f ̅(1_(R/kerf ) )=f ̅(1+kerf )=f(1_R )=1_S ○ f ̅((r_1+I)(r_2+I))=f ̅(r_1 r_2+I)=f(r_1 r_2 )=f(r_1 )f(r_2 )=f ̅(r_1+I) f ̅(r_2+I) • Example: R[x]\/(x^2+1)≅ℂ ○ Let F:R[x]→ℂ given by p↦p(i) ○ F is a ring homomorphism § In fact, if R is a subgring of some ring S, and s∈S, then § The function R[x]→S given by p↦p(s) is a ring homomorphism ○ F is surjective § If a+bi∈ℂ, then F(a+bx)=a+bi ○ (x^2+1)⊆kerf § If p(x^2+1)∈(x^2+1), then § F(p(x^2+1))=F(p)F(x^2+1)=p(i)p(i^2+1)=0 ○ kerf⊆(x^2+1) § Let p∈kerf § Using polynomial division, we can find q,r∈R[x] s.t. § p=q(x^2+1)+r where degr deg(x^2+1)=2 § Write r=ax+b for some a,b∈R § Since p∈kerf, p(i)=0 § 0=p(i)=q(i)×(i^2+1)+r(i)=r(i)=ai+b § So a=b=0 § Therefore p=q(x^2+1), and p∈(x^2+1) ○ Therefore, kerf=(x^2+1) ○ By the First Isomorphism Theorem of Rings, R[x]\/(x^2+1)≅ℂ • Example: R[x]\/(x−a)≅R, where a∈R ○ Let F:R[x]→R given by p↦p(a) ○ F is surjective § F(b)=b,∀b∈R ○ F is a ring homomorphism ○ (x−a)⊆kerf § If p(x−a)∈(x−a), then § F(p(x−a))=F(p)F(x−a)=p(a)p(a−a)=0 ○ kerf⊆(x−a) § Let p∈kerf § Divide x−a into p to obtain q,r∈R[x] s.t. § p=q(x−a)+r, where degr 1 § Since p∈kerf, 0=p(a)=q(a)(a−a)+r=r § Thus r=0, so p=q(x−a)∈(x−a) ○ Therefore, kerf=(x−a) ○ By the First Isomorphism Theorem of Rings, R[x]\/(x−a)≅R • Example: R[x]\/(x^2−1)≅R×R ○ Recall: Chinese Remainder Theorem § If I,J are ideals in a commutative ring R s.t. I+J=R § Then R\/IJ≅R\/I×R\/J, where § I+J={x+y│x∈I,y∈J} § IJ={x_1 y_1+…+x_n y_n│n∈Z(≥1),x_i∈I,y_i∈J} ○ (x^2−1)⊆(x+1)(x−1) § This is obvious, since x^2−1∈(x+1)(x−1) ○ (x+1)(x−1)⊆(x^2−1) § Let p_1 q_1+…+p_n q_n∈(x−1)(x+1), where p_i∈(x−1),q_i∈(x+1) § Each term p_i q_i is of form □ f_i (x−1)⋅g_i (x+1)=f_i g_i (x^2−1) for some f_i,g_i∈R § Thus p_i q_i∈(x^2−1)⇒p_1 q_1+…+p_n q_n∈(x^2−1) ○ Thus (x^2−1)=(x+1)(x−1) ○ R[x]\/(x+1)(x−1)≅R×R § 1/2 (x+1)−1/2 (x−1)=1∈R[x] § ⇒(x+1)+(x−1)=R[x] § ⇒1∈(x+1)+(x−1) § Chinese Remainder Theorem implies R[x]\/(x+1)(x−1)≅R×R ○ Therefore, R[x]\/(x^2−1)≅R×R Other Isomorphism Theorems for Rings • The Second Isomorphism Theorem for Rings ○ If I is an ideal of a ring R, and S is a subring of R ○ Then S+I is also a subring of R, where ○ I is an ideal of S+I, and (S+I)\/I≅S\/(I∩S) • The Third Isomorphism Theorem for Rings ○ If I⊆J are ideals of a ring R, then (R\/I)⁄(J\/I)≅R\/J • Correspondence Theorem ○ If R is a ring, and I is an ideal of R ○ Then there is a bijection {ideals of R\/I}⟷{ideals of R containing I}](https://shawnzhong.com/wp-content/uploads/2018/05/img_5aec790d90b90.png)

